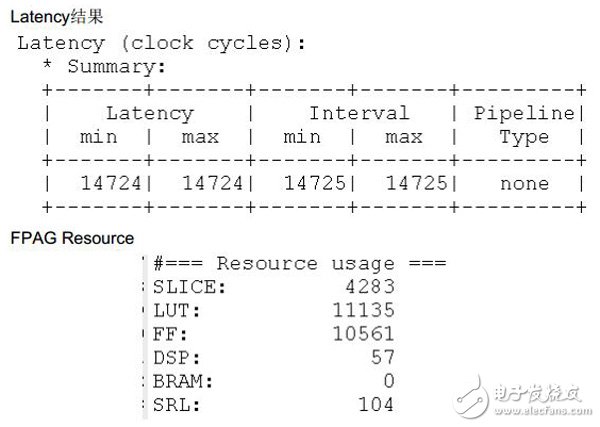
Floating point has a larger dynamic range of data, requiring only one data type advantage in many algorithms. This article describes how to implement floating point complex matrix decomposition using Vivado HLS. Using HLS, various matrix decomposition algorithms can be implemented quickly and efficiently, which greatly improves production efficiency and reduces the difficulty of the developer's algorithm FPGA implementation. Void matrix_dcmp Float diag[R_DIM], Coef_cal(lamda_sqrt, lamda, diag[i], pre_in_u, pd_err_in, &s_o,&s_conj_o,&la Cal_core(u_tmp, r_tmp, s_n, i, j, k, c_o, lamda_sqrtxc_o, lamda_sqrtxs_o, Void coef_calc Void calc_core The RTL code generated by Vivado-HLS retains the original c code hierarchy by default. When building the c code hierarchy, you can use the module division from top to bottom and bottom to top. Write the basic floating-point operations such as add, subtract, multiply, divide, square root, etc. into the lowest-level sub-function, and add a pipeline to it, even hit the register for better timing performance. The following example: Float hfmult In addition, in order to improve the parallelism of the operation, it is necessary to divide the in_u and r arrays in the matrix_dcmp (the HLS integrated into the BRAM or the distributed RAM of the FPGA) into the direcTIve, so that the data can travel to the parallel processing unit. 3, Vivado-HLS matrix decomposition timing optimization In order to make the in_u integrated RAM timing better, you can add the resource directive to the in_u integrated RAM to control it to 3 stages, so that the generated RAM input and output will hit a register. Similarly, we can also set the sufficient latency directive to DSP48, so that there is enough clock beat to give the DSP48 internal beat register. If the above-mentioned single-precision floating-point multiplication hfmult latency is set to 3, so that there is only 2 levels of latency allocated to each DSP48, then the integrated A_reg or P_reg inside the DSP48 will not be hit, so that the timing performance is Greatly dropped. or In order to achieve better timing performance, the above-mentioned single-precision floating-point multiplication hfmult latency is set to at least 4, so that there is only 3 levels of latency allocated to each DSP48, then the A_reg or P_reg inside the DSP48 will be combined. A beat. 4, Vivado-HLS matrix decomposition design results The size of the matrix in this design is 128x128 single precision floating point, complex number. Sfx Power Supply,Sfx 250W Power Supply,Sfx Pc 150W Power Supply,Psu 150W 200W Power Supply Boluo Xurong Electronics Co., Ltd. , https://www.greenleaf-pc.com
(
Cf_t in_u[(R_DIM+Y_DIM)/DIV_NUM][DIV_NUM],
Cf_t pd_err_in,
Float lamda,
Float lamda_sqrt,
Cf_t r[R_DIM][X_DIM],
Cf_t p[R_DIM]
)
{
Mda_sqrtxs_o,&c_o,&lamda_sqrtxc_o,&diag_out,&p_o,&pd_err);
S_conj_o, &in_u_w2, &r[i][r_addr]);
}
(
Float lamda_sqrt,
Float lamda,
Float r_diag,
Cf_t u_diag,
Cf_t pd_err_in,
Cf_t *s,
Cf_t *s_conj,
Cf_t *lamda_sqrtxs,
Float *c,
Float *lamda_sqrtxc,
Float *diag,
Cf_t *p_o,
Cf_t *pd_err
)
(
Cf_t in_u,
Cf_t r,
Int s_n,
Int i,
Unsigned char j,
Unsigned char k,
Float c_o,
Float lamda_sqrtxc_o,
Cf_t lamda_sqrtxs_o,
Cf_t s_conj_o,
Cf_t* u_ret,
Cf_t* r_ret
)
Template T reg(T x) {
#pragma HLS inline self off
#pragma HLS interface ap_none register port=return
Return x;
}
Cf_t mult( cf_t in1, cf_t in2 ) {
#pragma HLS PIPELINE
Cf_t out;
Float in1_re_in2_re, in1_im_in2_im, in1_re_in2_im, in1_im_in2_re;
In1_re_in2_re = hfmult(in1.re,in2.re);
In1_im_in2_im = hfmult(in1.im,in2.im);
In1_re_in2_im = hfmult(in1.re,in2.im);
In1_im_in2_re = hfmult(in1.im,in2.re);
Out.re = (in1_re_in2_re - in1_im_in2_im);
Out.im = (in1_re_in2_im + in1_im_in2_re);
Return reg(out);
}
(
Float in1,
Float in2
)
{
#pragma HLS PIPELINE
Float out;
Out = in1 * in2;
Return reg(out);
}
#pragma HLS ARRAY_PARTITION variable=in_u complete dim=2
#pragma HLS ARRAY_PARTITION variable=r complete dim=2
#pragma HLS RESOURCE variable=in_u core=RAM3S
Derive_core fmul_der -base FMul_maxdsp -latency 3 -fixed
Set_directive_resource -core fmul_der hfmult out 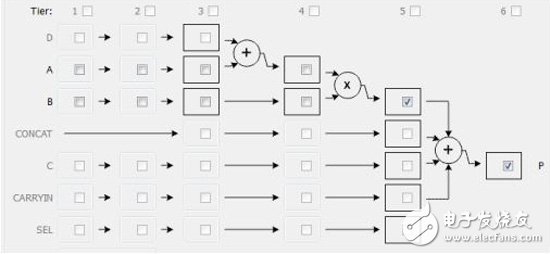
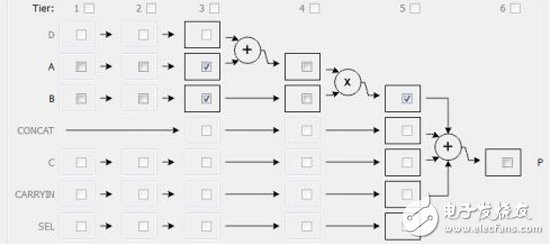
Derive_core fmul_der -base FMul_maxdsp -latency 4 -fixed
Set_directive_resource -core fmul_der hfmult out 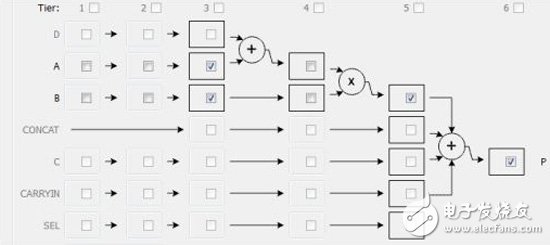
The combination of serial and parallel implementation is adopted.