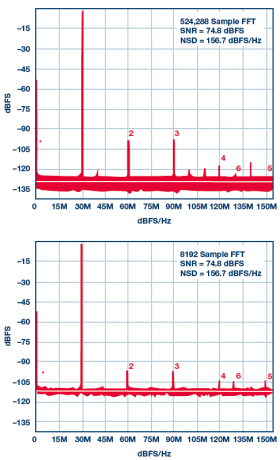
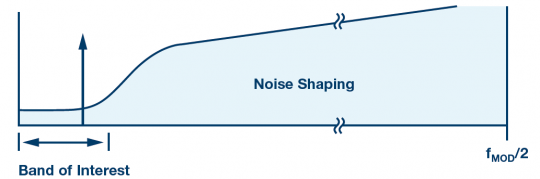
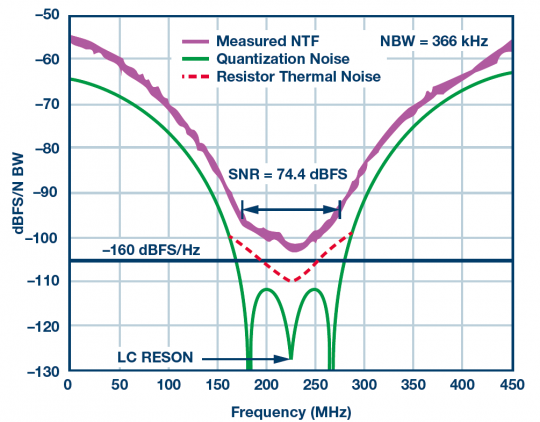
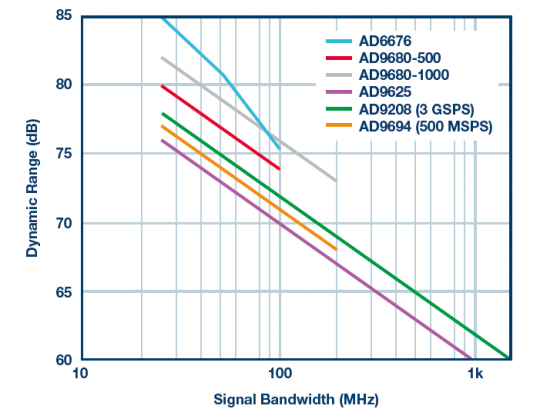
The ever-increasing number of high-speed and very high-speed ADCs and digital processing products are making oversampling a practical architectural approach to broadband and RF systems. Advances in semiconductor technology have contributed to speed and cost reductions (such as price, power consumption, and board area), allowing system designers to explore various ways of converting and processing signals—whether using flat noise spectral density Broadband converters use either band limited Σ-Δ converters with high dynamic range in the target band. These technologies have changed the design engineers' understanding of signal processing and how they define product specifications. Noise spectral density (NSD) and its distribution in the target frequency band allow it to be filtered out better during data conversion. . When comparing systems that operate at different speeds, or to see how software-defined systems handle signals of different bandwidths, noise spectral density (NSD) can be said to be more useful than signal-to-noise ratio (SNR). It cannot replace other specifications, but it will be a useful parameter indicator in the analysis toolbox. How much noise is in my target band? The SNR on the data converter data sheet represents the ratio of the full-range signal power to the total noise power of all other frequencies. Figure 1. Graphical representation of 9 dB modulation gain: All signals are preserved and 7â„8 noise is discarded. Now consider a simple case to compare SNR and NSD, as shown in Figure 1. Assume that the ADC clock frequency is 75 MHz. A fast Fourier transform (FFT) is run on the output data and the spectrum shown is from DC to 37.5 MHz. In this case, the target signal is the only large signal that happens to be near 2 MHz. For white noise (which in most cases includes quantization noise and thermal noise), the noise is evenly distributed within the Nyquist band of the converter, in this case, dc to 37.5 MHz. Since the target signal is between DC and 4 MHz, digital post-processing can be applied relatively easily to filter out or discard all frequencies above 4 MHz (only the contents in the red box are retained). Here will need to discard 7â„8 noise, keep all signal energy, so that effective SNR improves 9 dB. In other words, if you know that the signal is in half of the band, you can actually discard the other half of the band while only removing the noise. This leads to a useful rule of thumb: In the presence of white noise, the modulation gain can improve the SNR of the oversampled signal by an additional 3 dB/octave. In the example of Figure 1, this technique can be applied to three octaves (with a factor of 8) to improve the SNR by 9 dB. Of course, if the signal is somewhere between DC and 4 MHz, there is no need to use a fast 75 MSPS ADC to capture the signal. Only 9 MSPS or 10 MSPS can meet the bandwidth requirements of the Nyquist sampling theorem. In fact, one-eighth of 75 MSPS sampled data can be extracted, resulting in a 9.375 MSPS effective data rate while preserving the noise floor in the target band. It is important to extract properly. If only 7 samples are discarded every 8 samples, then the noise will be folded or aliased back into the target band, which will not get any SNR improvement. It must be filtered and then extracted to achieve the modulation gain. Even so, although the ideal filter eliminates all noise and achieves an ideal 3 dB/octave modulation gain, the actual filter does not have such characteristics. In practice, the amount of filter rejection required is a function of how much modulation gain is attempted to be achieved. It should also be noted that the "3 dB/octave" rule of thumb is based on the white noise assumption. This is a reasonable assumption, but it does not apply to all situations. One important exception is that the dynamic range is affected by nonlinear errors or other spurious intermodulation components in the passband. In these cases, the "filter and discard" method does not necessarily filter out spurious components and may require more elaborate frequency algorithms. Convert SNR and Sample Rate to Noise Spectral Density When there are multiple signals in the spectrum, such as many stations in the FM band, the situation becomes more complicated. To recover any signal, it is more important than the total noise of the data converter but the amount of converter noise that falls within the target frequency band. This requires digital filtering and post-processing to eliminate all out-of-band noise. There are several ways to reduce the amount of noise that falls into the red box. One of them is to choose an ADC with better SNR (lower noise). Or you can use an ADC with the same SNR and provide a faster clock (for example, 150 MHz), so that the noise is spread over a wider bandwidth and there is less noise in the red box. NSD enters the field of vision This raises a new question: Is there a better specification than SNR for a quick comparison of the filter's ability to filter out noise? The noise spectral density (NSD) will be used at this time. Spectral density (usually expressed in decibels relative to the full-scale decibel per Hertz bandwidth, ie, dBFS/Hz) is used to characterize the noise and the ADCs at different sample rates can be compared to determine which device may have the lowest noise in a particular application. . Table 1 uses a 70 dB SNR data converter as an example to illustrate how NSD improves as the sampling rate is increased from 100 MHz to 2 GHz. Table 1. Sample Rate for Changing a 70 dB SNR ADC Case Case Sample Rate Sample rate Nyquist BW Nyquist bandwidth SNR SNRNSD NSDSNR in 50 MHz Band 50 MHz SNROversampling Ratio for 50 MHz BW 50 MHz bandwidth oversampling rate A100 MSPS50 MHz70 dB–147 dBFs/Hz70 dB1 B500 MSPS250 MHz70 dB–154 dBFs/Hz77 dB5 C1 GSPS500 MHz70 dB–157 dBFs/Hz80 dB10 D2 GSPS1 GHz70 dB–160 dBFs/Hz83 dB20 Table 2 shows the various SNR and sampling rate combinations for some very different converters, but all combinations have the same NSD, so each combination will have the same total noise in the 1 MHz channel. Note that the actual resolution of the converter may be much higher than the effective number of bits because many converters want additional resolution to ensure that the quantization noise has a negligible effect on NSD. Table 2. Several very different converters provide 95 dB SNR in a 1 MHz bandwidth; SNR calculation assumes white noise floor (No spurious effects) Sample Rate Sample rate Nyquist BW Nyquist Bandwidth Number of Bits Number of SNR SNRNSD NSDSNR in 1 MHz Band 1 MHz band SNR Case 1 Case 1100 GSPS50 MHz848 dB–155 dBFs/Hz95 dB Case 2 Case 210 GSPS5 MHz10 to 12 10 to 1258 dB–155 dBFs/Hz95 dB Case 3 Case 31 GSPS500 MHz 1468 dB–155 dBFs/Hz95 dB Case 4 Case 4100 MSPS50 MHz 1478 dB–155 dBFs/Hz95 dB In a traditional single-carrier system, capturing a 1 MHz signal using a 10 GSPS converter may seem ridiculous, but in a multi-carrier software-defined system, that could be exactly what a designer would do. One example is a cable set-top box that may use a 2.7 GSPS to 3 GSPS full-range tuner to capture wired signals containing hundreds of television channels, each with a bandwidth of a few MHz. For data converters, the unit of noise spectral density is usually dBFS/Hz, which is dB relative to full scale per Hz. This is a relative measure that provides some kind of "fold to output" measurement of the noise level. There is also the use of dBm/Hz or even dBmV/Hz to provide a more absolute measure of the "converted to input" measurement of the data converter noise. SNR, full-scale voltage, input impedance, and Nyquist bandwidth can also be used to calculate the ADC's effective noise figure, but this involves quite complex calculations. See Analog Devices, Inc. guideline MT-006: "ADC Noise Figure - An Often Misunderstood parameters." Oversampling alternatives Using the ADC at a higher sampling rate usually means higher power consumption - whether it is the ADC itself or subsequent digital processing. Table 1 shows that oversampling is good for NSD, but the question remains: "Is oversampling really worth it?" As shown in Table 2, better NSD can also be achieved using a less noisy converter. Systems that capture multiple carriers need to operate at higher sampling rates and therefore oversampling each carrier. However, oversampling still has many advantages. Simplify Anti-Aliasing Filtering - Oversampling aliases higher frequency signals (and noise) into the Nyquist band of the converter. So for aliasing effects, these signals need to be filtered out by the filter before AD conversion. This means that the filter's transition band must be between the highest target capture frequency (FIN) and aliasing of that frequency (FSAMPLE, FIN). As the FIN gets closer to FSAMPLE/2, the transition band of this anti-aliasing filter becomes very narrow, requiring very high-order filters. Two to four times oversampling can drastically reduce this limitation in the analog domain and place the burden in a relatively easy-to-handle digital domain. Even with a perfect anti-aliasing filter, minimizing the effect of folding the converter's distortion product will also cause deficiencies, producing spurious and other distortion products in the ADC, including some very high-order harmonics. These harmonics will also fold within the sampling frequency and may return in-band, limiting the SNR within the target frequency band. At higher sampling rates, the desired frequency band becomes a fraction of the Nyquist bandwidth, thus reducing the probability of folding occurring. It is worth mentioning that oversampling also helps in the frequency planning of other system spurs (such as the device clock source) where in-band folding may occur. Modulation gain affects any white noise, including thermal noise and quantization noise, as well as noise from certain types of clock jitter. As higher-speed converters and digital processing products mature, system designers use a certain amount of oversampling more frequently to exploit these advantages, such as noise floor and FFT. Figure 2. 524,288 sample FFT and 8192 sample FFT ADC The user may wish to compare the converter by examining the spectral curve and looking at the noise floor depth, as shown in Figure 2. When making such comparisons, it is important to remember that the spectral curve depends on the size of the Fast Fourier Transform. Larger FFTs divide the bandwidth into more frequency bins, and less noise accumulates in each frequency bin. In this case, the spectrum curve shows a low noise floor, but this is only a drawing artifact. In fact, the noise spectral density has not changed (this is the signal processing equivalent of changing the resolution bandwidth of the spectrum analyzer). Finally, if the sampling rate is equal to the FFT size (or to an appropriate ratio), then comparing the noise floor is acceptable, otherwise misunderstanding may occur. Here, the NSD specification can be used for direct comparison. When the noise floor is not flat So far, the discussion of modulation gain and oversampling assumes that the noise is flat within the Nyquist band of the converter. This is a reasonable approximation in many cases, but there are some situations that do not apply this assumption. For example, it has been mentioned previously that modulation gain does not apply to spurious, although oversampling systems may have some advantages in frequency planning and spurious processing. In addition, 1/f noise and some types of oscillator phase noise have spectral shaping performance, and the modulation gain calculation is not suitable for such cases. Figure 3. Target frequency band and noise shaping An important situation where the noise is not flat is when using a Σ-Δ converter. The Σ-Δ modulator modulates the quantization noise by modulating the feedback loop (quantizer output) to reduce the noise in the target band, but at the cost of increasing the out-of-band noise, as shown in Figure 3. Even without a complete analysis, it can be seen that for a sigma-delta modulator, the use of NSD as a specification to determine the available in-band dynamic range is particularly effective. Figure 4 shows the noise floor curve of the high-speed, band-pass Σ-Δ ADC. In the 75 MHz target band (with a center frequency of 225 MHz), the noise is around -160 dBFS/Hz and the SNR exceeds 74 dBFS. Figure 4. AD6676 - Noise Floor A summary example To summarize and reinforce what we have already discussed, now look at the curve shown in Figure 5. This example considers five ADCs: a 12-bit, 2.5 GSPS ADC (purple curve); a 14-bit, 1.25 GSPS ADC with a clock speed of 500 MSPS (red curve); and 1 GSPS (green curve); A 14-bit, 3 GSPS ADC with a clock speed of 3 GSPS (gray curve); a different 14-bit, 500 MSPS ADC with a clock speed of 500 MSPS (blue curve); and finally the bandpass switch mentioned in Figure 4 Δ ADC. The first five cases are characterized by having a nearly white (flat) noise floor, while the Σ-Δ ADC has a bathtub-shaped noise spectral density with very low noise in the target band, as shown in Figure 4. In each case, the sampling rate remains fixed, and the signal bandwidth is scanned by changing the cutoff frequency of the digital filter (which removes the digitized out-of-band noise). From this we can draw a few conclusions. First, reducing the signal bandwidth increases the dynamic range. However, the slope of the purple, red, and green lines is always 3 dB/octave because its NSD curve is flat. The slope of the blue curve (Σ-Δ ADC) is quite steep. This phenomenon is particularly noticeable when the cut-off frequency of the decimation filter is scanned on a steep slope of the channel because each increment/decrement of this frequency results in a rapid change in the amount of filtered noise power. Second, each curve has a different vertical offset, depending on the NSD of the converter. For example, the red and green curves correspond to the same ADC. However, the green curve (1 GSPS) is higher than the red curve (500 MSPS) because its NSD is 3 dB/Hz lower than the others, and its clock is twice that of the red curve. Figure 5 shows the trade-off between SNR and signal bandwidth for many different high-speed ADCs: 5 slopes follow the flat 3 dB/octave modulation gain, and the AD6676 exhibits a steeper modulation gain due to noise floor shaping. Figure 5. Relationship between SNR and signal bandwidth of different ADCs Conclusion The ever-increasing number of high-speed and very high-speed ADCs and digital processing products are making oversampling a practical architectural approach to broadband and RF systems. Advances in semiconductor technology have contributed to speed and cost reductions (such as price, power consumption, and board area), allowing system designers to explore various ways of converting and processing signals—whether using flat noise spectral density Broadband converters use either band limited Σ-Δ converters with high dynamic range in the target band. These technologies have changed our understanding of signal processing and the way we define product specifications. Thinking about how to capture signals, engineers may think of comparing systems that work at different speeds. When making such comparisons or looking at how software-defined systems handle signals of different bandwidths, the noise spectral density can be said to be more useful than SNR. It cannot replace other specifications, but it will be a very useful item on the specification list. Vapesoul Rechargeable Vape Kit Vapesoul Rechargeable Vape Kit is so convenient, portable, and small volume, you just need to take them vapesoul rechargeable vape starter kit,vapesoul rechargeable vape kit battery,vapesoul rechargeable vape kit pen,vapesoul rechargeable vape kit device,vapesoul rechargeable vape kit mod Ningbo Autrends International Trade Co.,Ltd. , https://www.mosvapor.com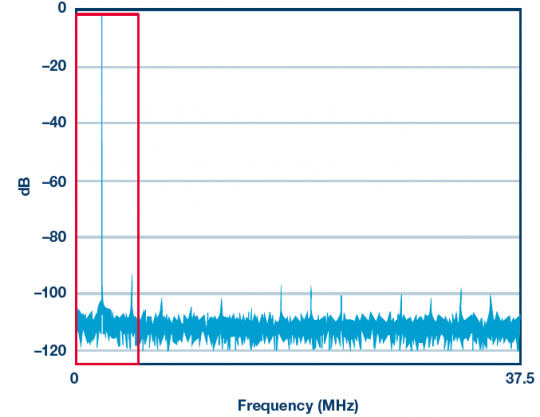
out of your pocket and take a puff, feel the cloud of smoke, and the fragrance of fruit surrounding you. It's so great.
We are the distributor of the Vapesoul & Voom vape brand, we sell vapesoul disposable vape,vapesoul vape bar, voom vape disposable, and so on.
We are also China's leading manufacturer and supplier of Disposable Vapes puff bars, disposable vape kit, e-cigarette
vape pens, and e-cigarette kit, and we specialize in disposable vapes, e-cigarette vape pens, e-cigarette kits, etc.