The traditional wavelet threshold image denoising method can remove part of the noise of the image and has better effect. However, due to the problem of the threshold function and the threshold selection method, the set threshold cannot completely remove the image noise, and it is also due to the threshold function. The problem is that the denoised image has poor visual effect. This requires improvement of the current threshold function and threshold selection method, and a wavelet threshold denoising method that can better remove image noise. 1.1, improvement of threshold function The two threshold functions mentioned above, the soft threshold function and the hard threshold function, although they can remove the image, have been widely used, but due to their own shortcomings, they still affect the image denoising effect. A disadvantage of the hard threshold function is that it is not continuous at the threshold point; the disadvantage of the soft threshold function is that there is a constant deviation between the original coefficient and the wavelet decomposition coefficient. These two threshold functions do not fully exhibit the energy distribution of the decomposed wavelet coefficients, which limits its further application. Therefore, a new threshold function needs to be sought to enable it to overcome the disadvantages of soft thresholds and hard thresholds while inheriting their advantages. This requires the threshold function to be continuous at its threshold point, and also has a high-order derivable property, so that the function of threshold value selection of the threshold function can be realized and the energy distribution of the coefficient after decomposition can be well represented. Based on the above analysis of the soft and hard thresholds and the high-order derivation of the exponential function, a new threshold function is now proposed, as follows: Where λ is the threshold. The two parameters p, q play their respective roles in the threshold function, which together determine the threshold process and results, where p ∈ [0, 1], q ≥ 0. This threshold function preserves the advantage that the soft threshold function has continuity in the wavelet domain and has a higher order derivative function when |x| ≥ λ. The threshold function plays a different role as p,q fluctuates within their respective fixed value intervals. When p=0, the threshold function becomes a hard threshold function regardless of the value of q; when p∈(0,1] and q=0, the threshold function becomes a soft threshold function; when p∈( 0,1] and q→∞, this threshold function becomes a threshold function similar to the soft threshold. In this function, the parameter p can adjust the degree of compression of the wavelet function by the threshold function, making up for the traditional soft threshold function. This is not enough. It can be seen that by changing the value of p, q, the effect of this threshold function on the wavelet coefficients can be determined. Wherein, the change of the q value mainly determines the trend of the threshold function, whether it is a soft threshold or a hard threshold, and the change of the p value mainly determines the degree of the effect of the threshold function on the wavelet coefficient. Through the joint action of the two parameters p and q, the threshold function becomes a soft threshold. A generalized function of the hard threshold overcomes the advantages of the two threshold functions while overcoming the wavelet coefficients. Some shortcomings. The newly proposed threshold function not only has continuity in the wavelet domain, but also has high-order derivable properties when |x|≥λ, so that the threshold function not only inherits the advantages of the continuity of the soft threshold function, but also overcomes the softness. The threshold has a disadvantage of inherent deviation between the wavelet coefficient and the original coefficient during processing, and also solves the problem that the fixed value compression of the coefficient larger than the threshold value and the noise decrease with the increase of the wavelet coefficient, and the problem is passed. The adjustment of the two parameters makes it have the performance of the hard threshold function at the same time, that is to say, the threshold function has the advantages of soft threshold and hard threshold, which is more convenient and flexible to use, and has better denoising effect. Another important factor in the wavelet threshold denoising method is the selection of the threshold. The threshold is mainly determined by the noise variance and the energy of the subband coefficients. In general, the noise variance needs to be derived from the observed data. If the threshold is too small, the noise removal is incomplete, and the image after denoising still has noise residual; if the threshold is selected too large, some signals are filtered out as noise, causing signal loss and causing deviation. The wavelet coefficients of noise decrease with the increase of the scale. Therefore, when denoising the signal, the thresholds of different decomposition layers should be selected differently, and the threshold should decrease as the decomposition scale increases. The traditional threshold selection methods, including the global threshold and the local adaptation threshold, have not changed with the change of the decomposition scale. Therefore, in view of the above requirements and the shortcomings of the traditional threshold selection method, a new one is proposed. Easy to implement threshold selection method: Where α is the standard deviation of Gaussian white noise, N is the image scale, and j is the decomposition scale. This threshold selection method is improved on the basis of the unified threshold. When the contribution of the standard deviation α and the image scale N on the threshold in the traditional unified threshold is retained, the decomposition scale j is added to the denominator, so that the threshold is The decomposition scale changes, and the larger the decomposition scale, the smaller the threshold value will be, which is more consistent with the fact that the coefficients of different decomposition layers after wavelet decomposition differ in the ratio distribution of signal and noise. The newly set threshold is based on the function of the original unified threshold in the threshold processing. With the newly added decomposition scale, the wavelet coefficients of each decomposition layer can be processed differently for different decomposition layers in the wavelet decomposition. This can increase the practicality of the threshold and reduce the deviation caused by the wavelet coefficient threshold mis-break. There are also several ways to select the standard deviation α of the white noise: it can be estimated by using the robust median estimation method. ==(median(|fi|)/0.6745)^(0.5) Where fi is the frequency band of the lowest decomposition scale ; the standard deviation of the diagonal detail coefficients in the wavelet decomposition coefficients can also be used as the estimated value of the noise standard deviation α. In this paper, the second method is adopted, and the standard deviation αD of the diagonal coefficient is used as the estimated value of α. In this way, the final threshold formula is: In the formula, αD is an estimated value of α, which can be easily calculated from the resolved diagonal coefficient after wavelet decomposition of the image signal. Hard and soft threshold methods have achieved good results in denoising, but they have disadvantages. Although equation (3) solves the error problem of |w^j,k-wj,k|, there is a discontinuity of ±λ, which will generate some additional oscillations during image reconstruction, and it is more prone to visual distortion such as Pseudo-Gibbs phenomenon. . Similarly, equation (4) has good continuity at ±λ, but there is a constant error in |w^j,k-wj,k|, which causes distortion of the high-frequency information of the image, and the equation (4) There is a difficulty in high-order derivation, which is not conducive to further processing it with mathematical tools. The hard and soft compromise threshold function improves the equation (3)(4), but there is still a constant deviation problem.
BIOTEPT NEMA Brake AC motors stop equipment when power to the motor is stopped and are used for applications that require rapid stopping and holding action. They also provide braking as a safety measure if power is cut abruptly. Motors are commonly used on conveyors, door operators, hoists, machine tools, and speed reducers that require quick stops or to prevent equipment rollback
Nema Brake Motor,Brek Motor,Capacitor Start Motor,Single Phase Capacitor Ningbo Biote Mechanical Electrical Co.,Ltd , https://www.biotept.com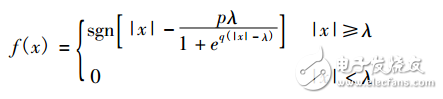
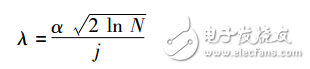
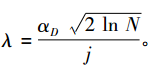



1. Improvement of wavelet threshold denoising