This article aims at the online simulation of the inverted pendulum swing angle controller in the course design of the undergraduate automatic control principle: the swing of the swing lever is unsafe, the single variable swing angle controller cannot control the position of the car at the same time, and the experimental observation is inconvenient. In this paper, a combined control system based on Goku's swing control, optimal trolley position control, and embedded student swing angle control is proposed and designed. Online simulation experiments show that the combined control system is effective for the control of the straight-line inverted pendulum, and can meet the requirements of undergraduate automatic control theory courses that do not take into account the safety, automation, intuitiveness, speed, and reliability of the experiment. The experimental system of the linear first-level inverted pendulum is shown in Figure 1. Based on the force analysis of the trolley and the pendulum, according to Newton's law of motion, the dynamic model of the linear first-order inverted pendulum can be obtained as shown in equation (1). 2 Design of embedded combination controller 2.1 Analysis of system controllability Automatic swing controller Swing-up Controller can control the straight-line inverted pendulum from the stable stable state of static drooping to the unstable state of vertical upward, without the need to apply force to the swing bar, the swing bar can be realized Automatically swings up. Solar Street Light,High Quality Solar Street Light,Solar Street Light Details, Yangzhou Bright Solar Solutions Co., Ltd. Yangzhou Bright Solar Solutions Co., Ltd. , https://www.cnbrightsolar.com
1 System modeling The control goal of the linear first-level inverted pendulum system is that the deflection angle of the pendulum rod does not exceed ± 5 °, and the left and right deviation of the trolley in the middle of the track does not exceed ± 10 cm, so as to achieve a dynamic balance.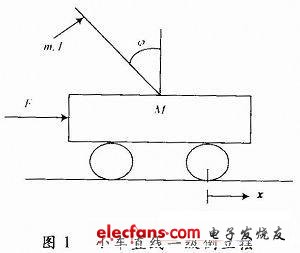 
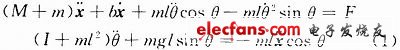
In the formula: M is the mass of the trolley, m is the mass of the pendulum; b is the friction coefficient of the trolley; l is the length of the pendulum; I is the moment of inertia of the pendulum; .
Since θ = π + φ, and φ≤1 (converted to radian comparison), u represents the input force F of the controlled object, then linearize the equation (1) to obtain the equation (2), as follows: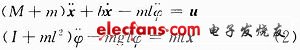 
Swing the rod evenly for the quality, take 
, The state space of the system from linear system theory is shown in equation (3):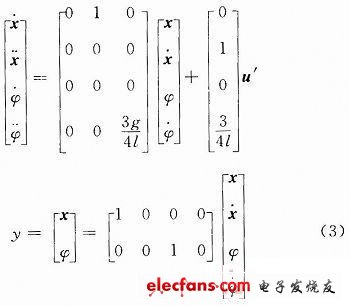 
The controlled system state fully controllable matrix Uc = [B AB A2BA3B], through calculation we can get rank (Uc) = 4, that is, the rank of the matrix Uc is equal to the dimension of the system state variable; the controlled system outputs the fully controllable matrix Uo = [CB CAB CA2B CA3B D], find rank (Uo), that is, the rank of the matrix Uo is equal to the dimension of the system output vector. So the system is controllable, and the controller can be designed to make the system stable.
The controller used in this article is an embedded combination controller composed of an automatic swing controller Swingup Controller, a linear secondary regulator LQR Controller and a controller Controller1 designed by students. Build a linear one-stage inverted pendulum embedded combined control system in Simulink, as shown in Figure 2. 